2020. 10. 2. 17:15ㆍProblem Solving/백준
문제
풀이
히스토그램 문제에 스택과 세그먼트 트리를 사용한 풀이가 있는데, 세그먼트 트리를 사용하여 풀어보겠습니다.
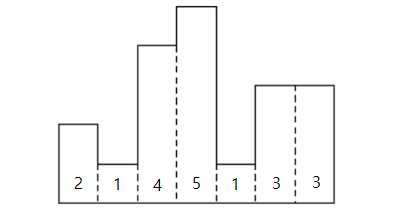
위와 같은 히스토그램이 있습니다.
아래와 같은 분할 정복을 사용하여 문제를 풀어보겠습니다.
* 구간 [left, right]를 정복하고 있을 때,
- 해당 구간에서 최소 높이를 h라고 두고, 높이가 h인 직사각형의 인덱스를 i라고 하겠습니다.
- (right - left + 1) * h가 답이 될 수 있습니다.
- 그리고 구간 [left, i - 1]과 [i + 1, right]에서 다시 분할 정복을 해나가면 됩니다.
테스트케이스를 예시로 설명해보겠습니다.
[1, 7]을 정복하고 있을 때
2번째 직사각형의 높이가 1로 가장 작으니(최솟값이 여러개 있으면 아무거나 선택해도 상관 없습니다.), 2번째 직사각형을 기준으로 분할 정복을 하겠습니다.
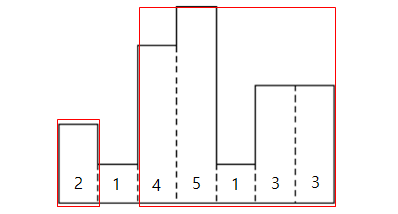
높이를 1로 가지는 직사각형의 넓이인 7 * 1 = 7이 있고, 2번째 직사각형을 포함하지 않는 두 구간으로 나눠 탐색을 계속 합니다.
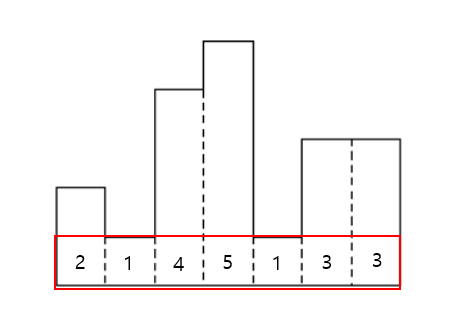
[1, 1]를 정복하고 있을 때
1번째 직사각형의 높이가 2이므로, 넓이는 2 * 1 = 2가 됩니다.
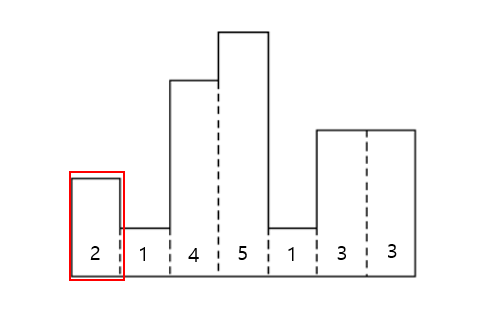
[3, 7]를 정복하고 있을 때
5번째 직사각형의 높이가 1이므로, 높이가 1이고 너비가 5인 직사각형이 있습니다. (넓이: 1 * 5 = 5)
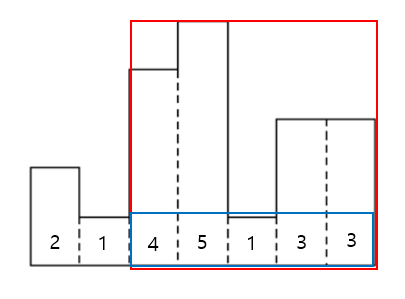
다음은 5번째 직사각형을 기준으로 분할정복을 하겠습니다.
[3, 4]를 정복하고 있을 때
3번째 직사각형의 높이가 4이므로, 높이가 4이고 너비가 2인 직사각형이 있습니다. (넓이: 2 * 4 = 8)
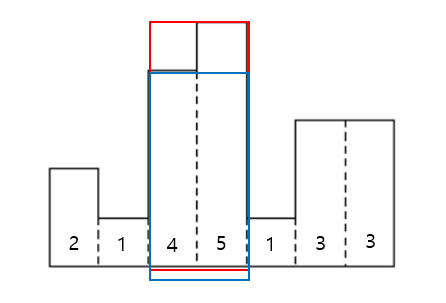
3번째 직사각형을 기준으로 분할 정복을 하면 [4, 4]만 분할 정복을 하게 되는데, 즉 4번째 직사각형의 높이가 넓이가 됩니다.
따라서 5번째 직사각형의 넓이는 5입니다.
[6, 7]을 정복하고 있을 때
6번째 직사각형의 높이가 3이므로, 높이가 3이고 너비가 2인 직사각형이 있습니다. (넓이: 3 * 2 = 6)
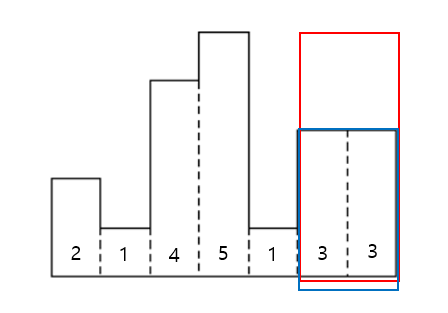
6번째 직사각형을 기준으로 분할 정복을 하면 [7, 7]만 분할 정복을 하게 되는데, 즉 7번째 직사각형의 높이가 넓이가 됩니다.
따라서 7번째 직사각형의 넓이는 3입니다.
분할 정복을 재귀적으로 실행하며, [3, 4]를 정복하고 있을 때 직사각형의 넓이가 8로 가장 큰 것을 알 수 있습니다.
위 과정을 아래 그림으로 정리해보았습니다.
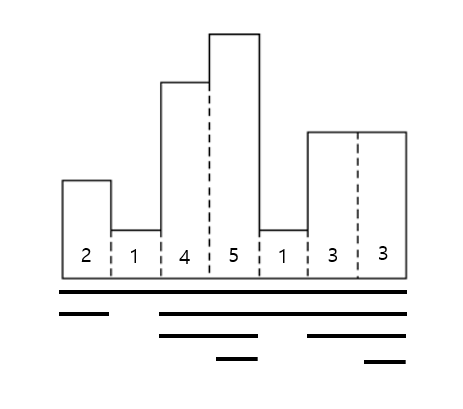
또한, 분할 정복을 실행할 때 구간에서 가장 작은 직사각형의 높이는 세그먼트 트리의 대푯값을 최소의 높이를 가지는 직사각형의 인덱스로 놓으면 $ O(log N) $에 구할 수 있습니다.
소스코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll arr[100001], seg[400001];
ll init(int node, int start, int end) {
if (start == end) return seg[node] = start;
int mid = start + end >> 1;
int a = init(node * 2, start, mid), b = init(node * 2 + 1, mid + 1, end);
if (arr[a] > arr[b]) return seg[node] = b;
else return seg[node] = a;
}
ll find(int node, int start, int end, int left, int right) {
if (start > right || end < left) return 0; //1e10
if (left <= start && end <= right) return seg[node];
int mid = start + end >> 1;
int a = find(node * 2, start, mid, left, right), b = find(node * 2 + 1, mid + 1, end, left, right);
if (arr[a] > arr[b]) return b;
else return a;
}
ll query(ll left, ll right) {
if (left > right) return 0;
int index = find(1, 1, n, left, right);
ll ans = (right - left + 1) * arr[index];
ans = max(ans, query(left, index - 1));
ans = max(ans, query(index + 1, right));
return ans;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cout.tie(0);
arr[0] = 1e10;
while (1) {
cin >> n;
if (!n) break;
for (int i = 1; i <= n; i++) cin >> arr[i];
init(1, 1, n);
cout << query(1, n) << "\n";
}
}
'Problem Solving > 백준' 카테고리의 다른 글
| 백준 2881번, 산책길 풀이 (0) | 2020.10.05 |
|---|---|
| 백준 1396번 (병렬 이분 탐색/PBS), 크루스칼의 공 (0) | 2020.10.03 |
| 백준 14428번, 수열과 쿼리 16 (0) | 2020.10.01 |
| 백준 9997, 폰트 풀이 (0) | 2020.09.30 |
| 백준 14462, 소가 길을 건너간 이유 8 (0) | 2020.09.29 |