2020. 9. 27. 16:41ㆍProblem Solving/백준
문제
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 �
www.acmicpc.net
크루스칼 알고리즘
3 3
1 2 1
2 3 2
1 3 3테스트 케이스의 내용을 시각화하면 아래와 같습니다.
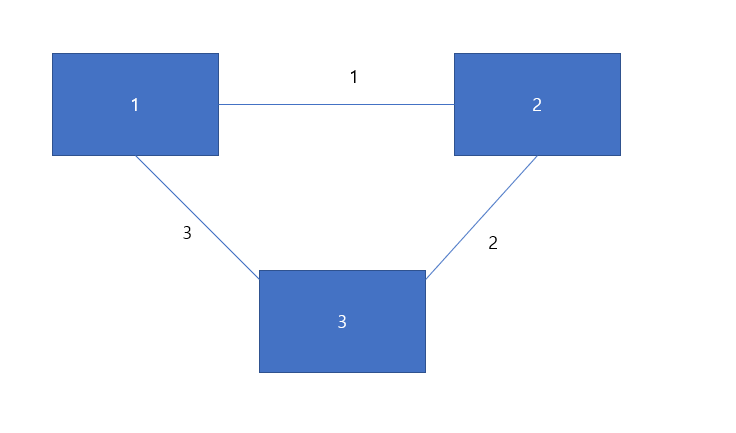
트리 구조를 유지하되, 간선의 가중치를 최소화하려면 (1, 3)의 간선을 제거하면 됩니다.
크루스칼 알고리즘은 최소 비용 신장 트리를 찾는 알고리즘입니다.
작동 방법을 설명하기 위해 아래 그래프의 최소 스패닝 트리를 구해보겠습니다.
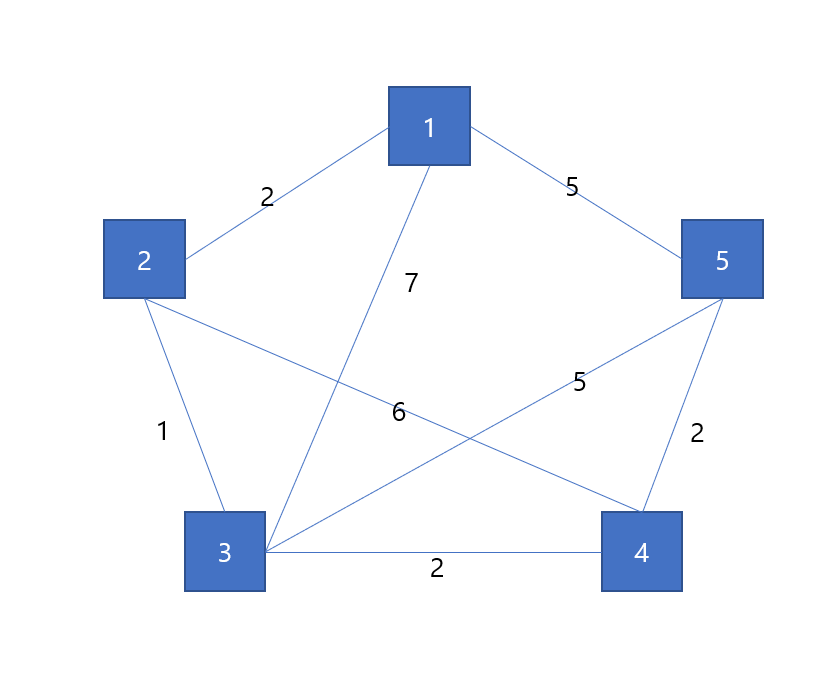
우선, 간선의 가중치가 오름차순이 되도록 정렬을 실행합니다.
|
가중치 (w) |
정점 (u) |
정점 (v) |
|
1 |
2 |
3 |
|
2 |
1 |
2 |
|
2 |
3 |
4 |
|
2 |
4 |
5 |
|
5 |
1 |
5 |
|
5 |
3 |
5 |
|
6 |
2 |
4 |
|
7 |
1 |
3 |
그 다음, 가중치가 작은 간선부터 새로 트리를 구성하겠습니다.
여기서 가중치가 작은 순으로 간선을 이을 때마다, union-find를 실행합니다.
1. find > 간선의 양 끝점(u, v)에 find 연산을 실행해서 root 노드가 같으면, 이미 두 정점은 가중치가 더 작은 간선으로 연결이 되었기 때문에 추가하지 않습는다. (추가하면 순환하기 때문이다), 실행할 때마다 path compression을 사용하여 시간을 줄일 수 있습니다.
2. union (merge) > 간선의 양 끝점(u, v)에 대해 union 연산을 실행해서 묶습니다..
가중치가 제일 작은 1은 (2, 3)을 잇는 간선입니다.
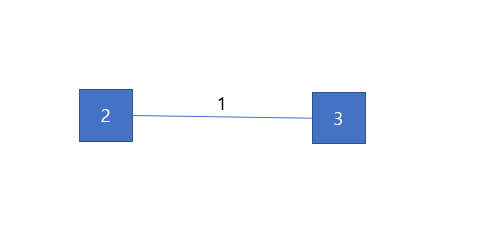
find(2) = 2, find(3)=3, 따라서, 2와 3은 같은 집합에 속하지 않으므로 트리의 구조를 유지할 수 있다.
union(2, 3)을 실행하여 두 노드를 묶는다.
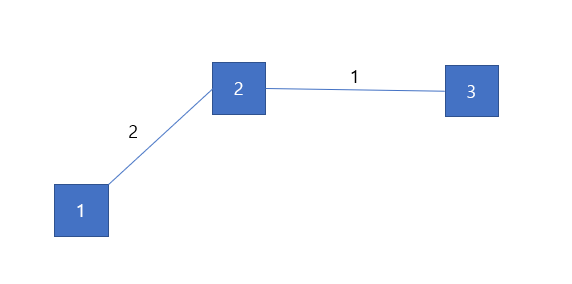
가중치가 2이고, (1, 2)인 간선을 추가해도 트리의 구조를 유지하므로 계속 추가합니다.
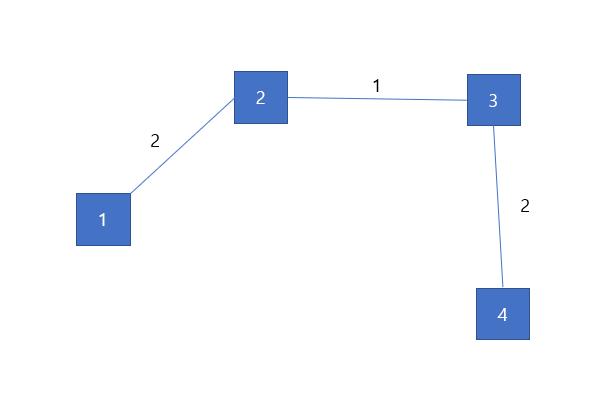
여전히, 가중치가 2이고, (3,4)인 간선을 추가해도 트리의 구조를 유지합니다.
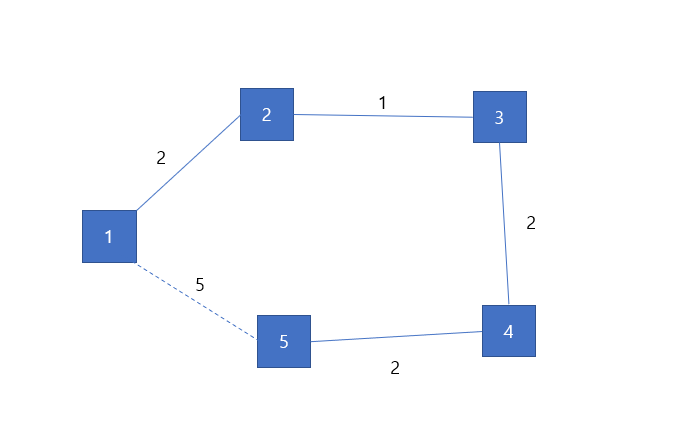
위와 같은 방식으로 계속 추가하다 보면, 위와 같이 순환하는 경우가 있습니다. (가중치가 5이고, (1,5)를 연결하는 간선)
코드로는 find(1)과 find(5)가 같은 경우일 때를 따로 빼면 됩니다.
계속 같은 방식으로 추가해도, 위와 같이 순환하는 경우만 생기므로 위 그래프의 최소 스패닝 트리는 아래와 같습니다.
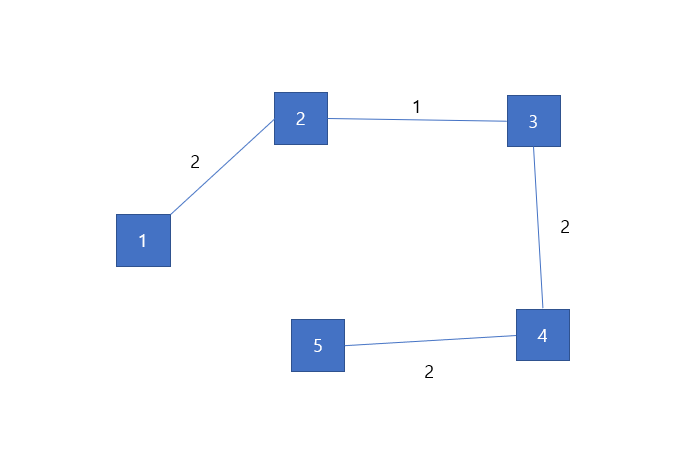
크루스칼 알고리즘을 사용하여 https://www.acmicpc.net/problem/1197를 아래의 코드로 풀 수 있습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct A {
int u, v, w;
bool operator<(const A& b) {
return w < b.w;
}
};
vector<A> graph;
vector<int> root;
int ans = 0;
int find(int a) {
if (root[a] == a) return a;
else return root[a] = find(root[a]);
}
int merge(int a, int b) {
int x = find(a), y = find(b);
if (x != y) {
root[x] = y;
return 1;
}
return 0;
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int v, e; cin >> v >> e;
for (int i = 0; i <= v; i++) root.push_back(i);
for (int i = 0; i < e; i++) {
int a, b, c; cin >> a >> b >> c;
graph.push_back(A{ a,b,c });
}
sort(graph.begin(), graph.end());
for (A a : graph) {
if (merge(a.u, a.v)) {
ans += a.w;
}
}
cout << ans;
}
'Problem Solving > 백준' 카테고리의 다른 글
| 백준 14462, 소가 길을 건너간 이유 8 (0) | 2020.09.29 |
|---|---|
| 백준 1806번, 부분합 풀이 (0) | 2020.09.28 |
| 백준 12930번, 두 가중치 풀이 (0) | 2020.09.27 |
| 백준 8983번, 한국정보올림피아드(KOI) 2013 고등부 1번, 사냥꾼 풀이 (0) | 2020.09.27 |
| 백준 5550번 (JOI 2011년 2번), 헌책방 풀이 (0) | 2020.09.27 |